Unit Imaginary Number. The square root of minus one √ (−1) is the “unit” Imaginary Number, the equivalent of 1 for Real Numbers. In mathematics the symbol for √ (−1) is i for imaginary. But in electronics the symbol is j, because i is used for current, and j is next in the alphabet.
Apartments for Sale and Property for Sale from Balwin
Math Algebra Algebra solutions manuals College Algebra 7th edition chapter 1.5 problem 1E We have solutions for your book! This problem has been solved: Problem 1E Chapter CH1.5 Problem 1E The imaginary number i has the property that i2 = _________. Step-by-step solution 100% (5 ratings) for this solution Chapter 1.5, Problem 1E is solved.
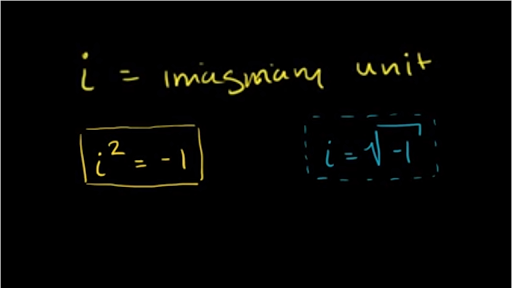
Source Image: khanacademy.org
Download Image
7,738 solutions Precalculus with Limits 3rd Edition • ISBN: 9781133962885 (1 more) Larson 11,147 solutions Precalculus: Mathematics for Calculus 7th Edition • ISBN: 9781305071759 (2 more) Lothar Redlin, Stewart, Watson 8,797 solutions

Source Image: slideplayer.com
Download Image
imaginary-numbers | Number worksheets, Complex numbers, Worksheets Once you expand the binomial, you will have two real terms and two imaginary terms (the i squared term is a real term since i^2=-1). THen you combine like terms. Since the two numbers you wrote are “conjugates” of each other, the imaginary terms will be opposites of each other and your answer will just be the real number (-2)^2 + 1^2 = 4 + 1 =5.

Source Image: pinterest.com
Download Image
The Imaginary Number I Has The Property That I2
Once you expand the binomial, you will have two real terms and two imaginary terms (the i squared term is a real term since i^2=-1). THen you combine like terms. Since the two numbers you wrote are “conjugates” of each other, the imaginary terms will be opposites of each other and your answer will just be the real number (-2)^2 + 1^2 = 4 + 1 =5. (And some ideas) My questions are about the way that I’m trying to come up with a proof to the equation i²=-1 (and from there maybe also the equation sqrt (-1)=i or –i) without of course first accepting them to be true axiomatically. I would like to hear your ideas!
Imaginary Numbers – i CHART | Math tricks, Chart, Complex numbers
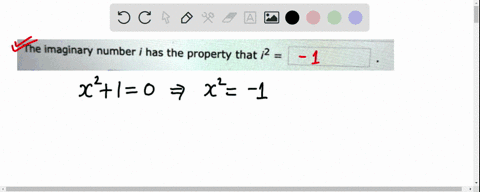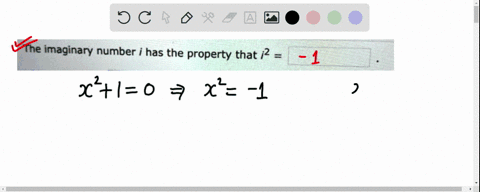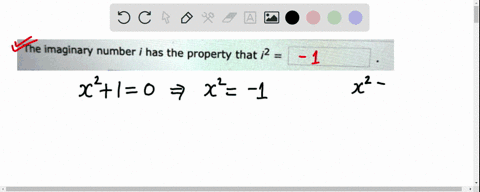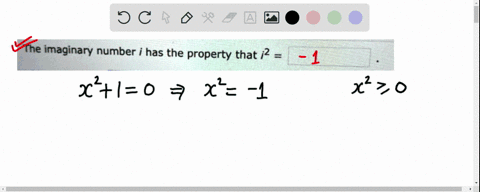
Algebra and Trigonometry (3rd Edition) Edit edition Solutions for Chapter 1.4 Problem 1E: The imaginary number i has the property that i2 = _____. … Solutions for problems in chapter 1.4 1E ⏩SOLVED:The imaginary number i has the property that i^2= . | Numerade
Source Image: numerade.com
Download Image
The Age of AI has begun | Bill Gates Algebra and Trigonometry (3rd Edition) Edit edition Solutions for Chapter 1.4 Problem 1E: The imaginary number i has the property that i2 = _____. … Solutions for problems in chapter 1.4 1E

Source Image: gatesnotes.com
Download Image
Apartments for Sale and Property for Sale from Balwin Unit Imaginary Number. The square root of minus one √ (−1) is the “unit” Imaginary Number, the equivalent of 1 for Real Numbers. In mathematics the symbol for √ (−1) is i for imaginary. But in electronics the symbol is j, because i is used for current, and j is next in the alphabet.

Source Image: balwin.co.za
Download Image
imaginary-numbers | Number worksheets, Complex numbers, Worksheets 7,738 solutions Precalculus with Limits 3rd Edition • ISBN: 9781133962885 (1 more) Larson 11,147 solutions Precalculus: Mathematics for Calculus 7th Edition • ISBN: 9781305071759 (2 more) Lothar Redlin, Stewart, Watson 8,797 solutions

Source Image: pinterest.ca
Download Image
Report: The war in Tigray is undermining its environmental recovery – CEOBS About Transcript Learn about the imaginary unit, “i“, a unique number defined as the square root of -1. It’s a key part of complex numbers, which are in the form a + bi. The powers of “i” cycle through a set of values. Created by Sal Khan. Questions Tips & Thanks Want to join the conversation? Sort by: Top Voted fuller.jeremiah 12 years ago

Source Image: ceobs.org
Download Image
AI in Real Estate: Transforming the Future of Property Once you expand the binomial, you will have two real terms and two imaginary terms (the i squared term is a real term since i^2=-1). THen you combine like terms. Since the two numbers you wrote are “conjugates” of each other, the imaginary terms will be opposites of each other and your answer will just be the real number (-2)^2 + 1^2 = 4 + 1 =5.

Source Image: radixweb.com
Download Image
Mapped: The State of Economic Freedom in 2023 (And some ideas) My questions are about the way that I’m trying to come up with a proof to the equation i²=-1 (and from there maybe also the equation sqrt (-1)=i or –i) without of course first accepting them to be true axiomatically. I would like to hear your ideas!

Source Image: visualcapitalist.com
Download Image
The Age of AI has begun | Bill Gates
Mapped: The State of Economic Freedom in 2023 Math Algebra Algebra solutions manuals College Algebra 7th edition chapter 1.5 problem 1E We have solutions for your book! This problem has been solved: Problem 1E Chapter CH1.5 Problem 1E The imaginary number i has the property that i2 = _________. Step-by-step solution 100% (5 ratings) for this solution Chapter 1.5, Problem 1E is solved.
imaginary-numbers | Number worksheets, Complex numbers, Worksheets AI in Real Estate: Transforming the Future of Property About Transcript Learn about the imaginary unit, “i“, a unique number defined as the square root of -1. It’s a key part of complex numbers, which are in the form a + bi. The powers of “i” cycle through a set of values. Created by Sal Khan. Questions Tips & Thanks Want to join the conversation? Sort by: Top Voted fuller.jeremiah 12 years ago